深度学习五:循环神经网络
为什么需要RNN
循环神经网络(Recurrent Neural Network,RNN)是一种用于处理序列数据的神经网络模型。与传统的前馈神经网络不同,RNN具有循环连接,使其可以处理具有时间相关性的数据。
对于全连接层,它能处理的只是一个个输入,前一个输入和后一个输入时完全没有关系的,但是某些地方任务需要能够更好的处理序列的信息,即是前面的输入和后面的输入是有关系的。这个时候我们就希望神经网络是有记忆的,那怎么办呢,就把之前得到的特征传进来就可以了是吧,的确是的。
RNN结构
来看一个简单的循环神经网络,有一个输入层、一个隐藏层和一个输出层组成:
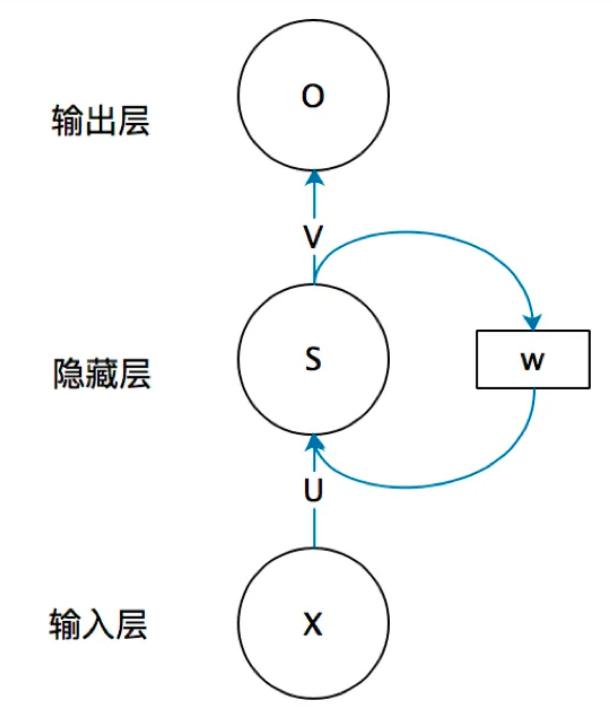
如果说我们把w去掉,那么它就是一个普普通通的线性层了吗,非常正确,它就相当于加了一个w,那么w是一个什么东西呢?要记住前面的特征,所以他应该含有前面的特征向量,所以w就包含了前面的特征信息。展开来看就是下面的图:
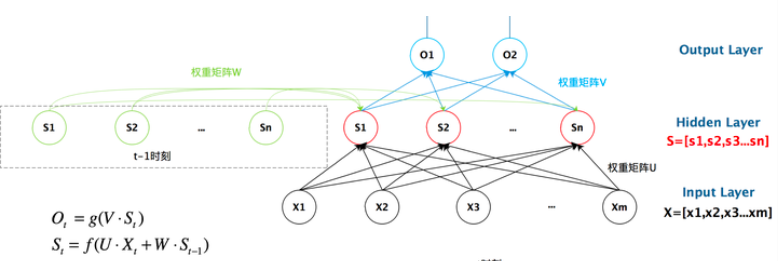
我们可以清晰看到,上一个时刻隐藏层会把自己的数据加到当前的输入上,然后通过一个激活函数。我们把上面的图展开,循环神经网络可以画成下面的这个样子:
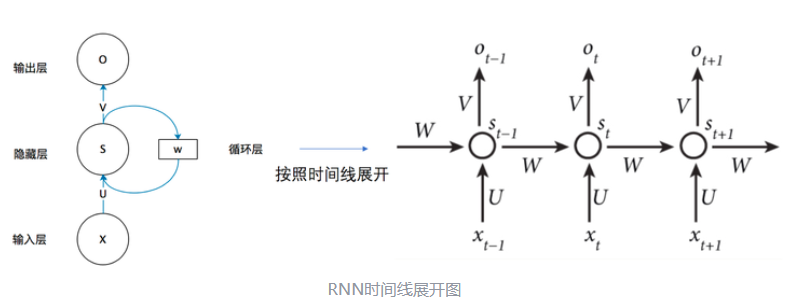


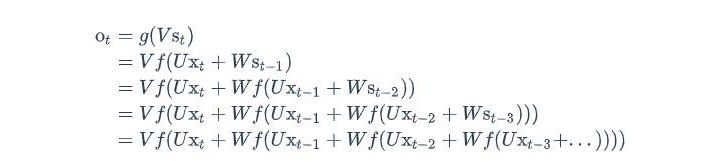

双向RNN
我们有个问题,我的RNN的方向目前来看是从前往后的,但是有些后面的序列对前面的影响很重要,我们是不是可以添加一个循环神经网络,然后正向反向都得到一个特征序列,然后把两个RNN的隐藏层都拿出来给一个输出层,得到最后的y。


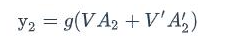

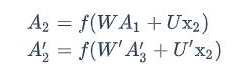

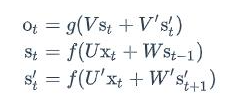
正向计算和反向计算不共享权重,也就是说U和U’、W和W’以及V和V’都是不同的权重矩阵。
循环神经网络的训练算法:BPTT
BPTT算法是针对循环层的训练算法,它的基本原理和BP算法是一样的,也包含同样的三个步骤:
- 前向计算每个神经元的输出值;
- 反向计算每个神经元的误差项δj值,它是误差函数E对神经元j的加权输入netj的偏导数;
- 计算每个权重的梯度。
最后再用随机梯度下降算法更新权重。
循环层如下图所示:
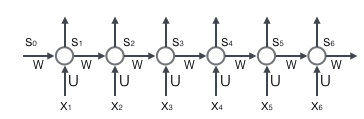
前向计算:
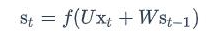
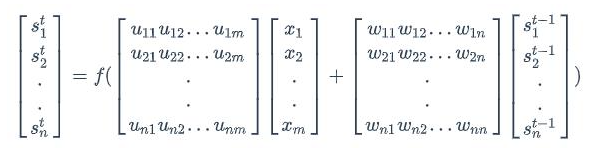
注意上面的s~t~、x~t~和s~t-1~都是向量;而U和V是矩阵,用大写字母表示。我们假设输入向量x的维度是m,输出向量s的维度是n,则矩阵U的维度是n*m,矩阵W的维度是n*m,下面是式子展开成矩阵的样子,看起来更加直观一些:
误差项计算

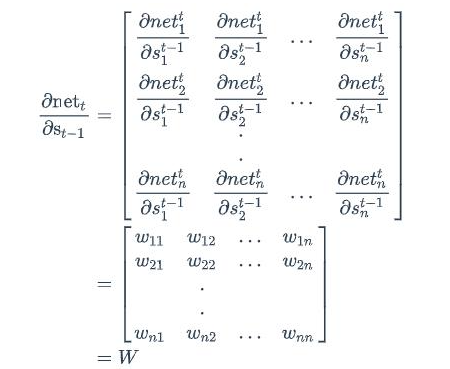
同样的,上式第二项可以写为:

其中diag[a]表示的是根据向量a创建一个对角矩阵,即:
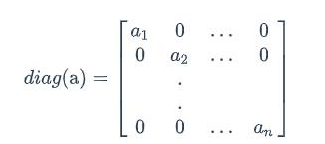
最后,将两项合在一起,可得:

上式描述了将$vartheta$沿时间往前传递一个时刻的规律,有了这个规律,我们就可以求得任意时刻k的误差项$vartheta_k$:

将误差项反向传递到上一层网络,就是和全连接层是一样的。循环层的加权输入net^l^与上一层的加权输入net^l-1^的关系如下:
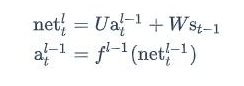
推不下去了!!!
LSTM

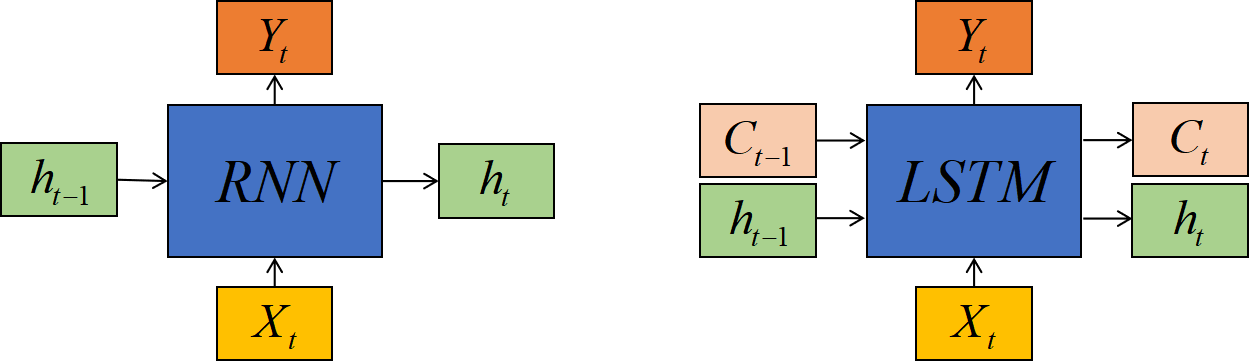


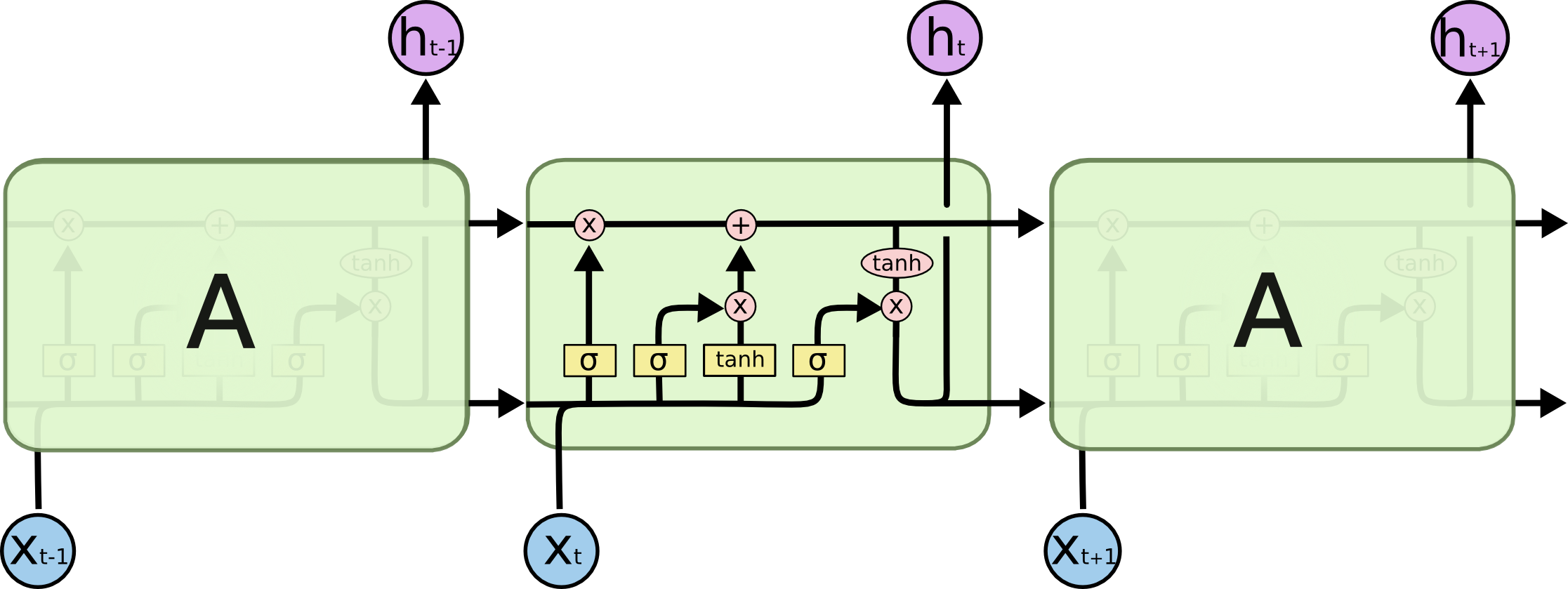
这是一个复杂的流程,但在横向上,它可以被分割为C的传递和h的传递两条路径;在纵向上,它可以被分为如图所示的三个不同的路径:
1. 帮助循环网络选择吸纳多少新信息的输入门
2. 帮助循环网络选择遗忘多少历史信息的遗忘门
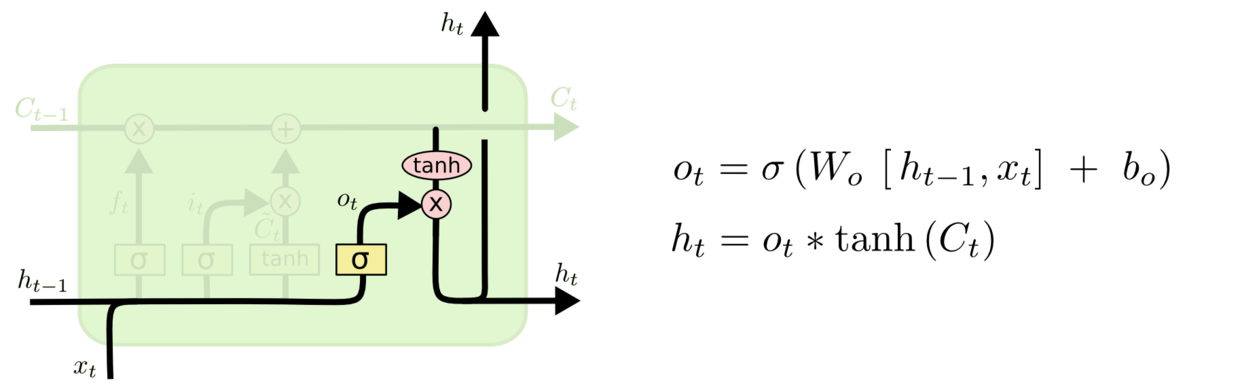
3. 帮助循环网络选择出对当前时间步的预测来说最重要的信息、并将该信息输出给当前时间步的输出门

让我们分别来看一下三个门是如何工作的。

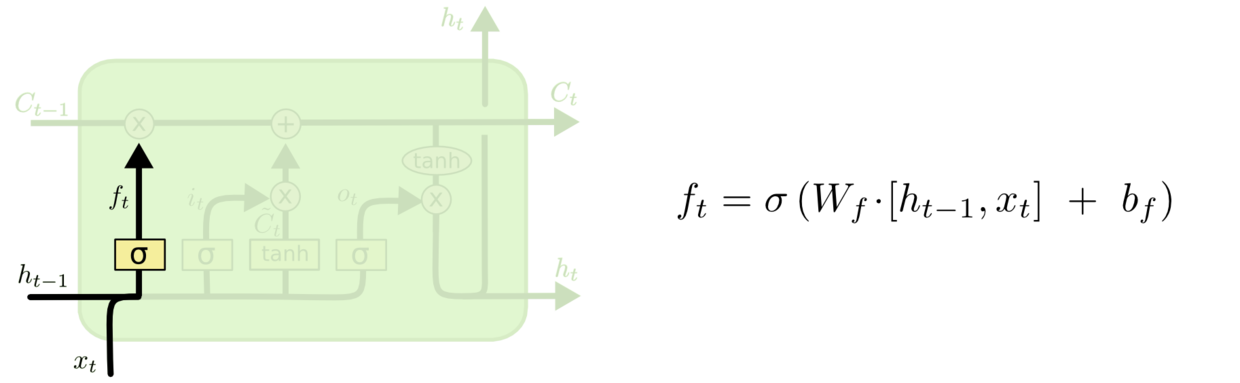





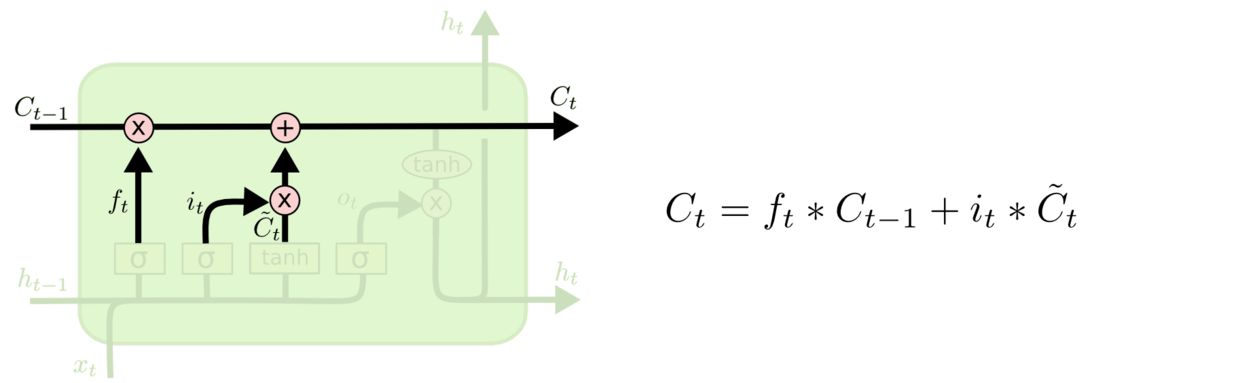


RNN为什么容易梯度爆炸和梯度消失
梯度消失和梯度爆炸是RNN在反向传播过程中常见的问题,RNN的反向传播是通过时间的反向传播”(Backpropagation Through Time,BPTT),其运行流程与一般的反向传播大有不同。在之前的课程中我们提到,在不同类型NLP任务会有不同的输出层结构、会有不同的标签输出方式。例如,在对词语/样本进行预测的任务中(情感分类、词性标注、时间序列等任务),RNN会在每个时间步都输出词语对应的相应预测标签;但是,在对句子进行预测的任务中(例如,生成式任务、seq2seq的任务、或以句子为单位进行标注、分类的任务),RNN很可能只会在最后一个时间步输出句子相对应的预测标签。输出标签的方式不同,反向传播的流程自然会有所区别。


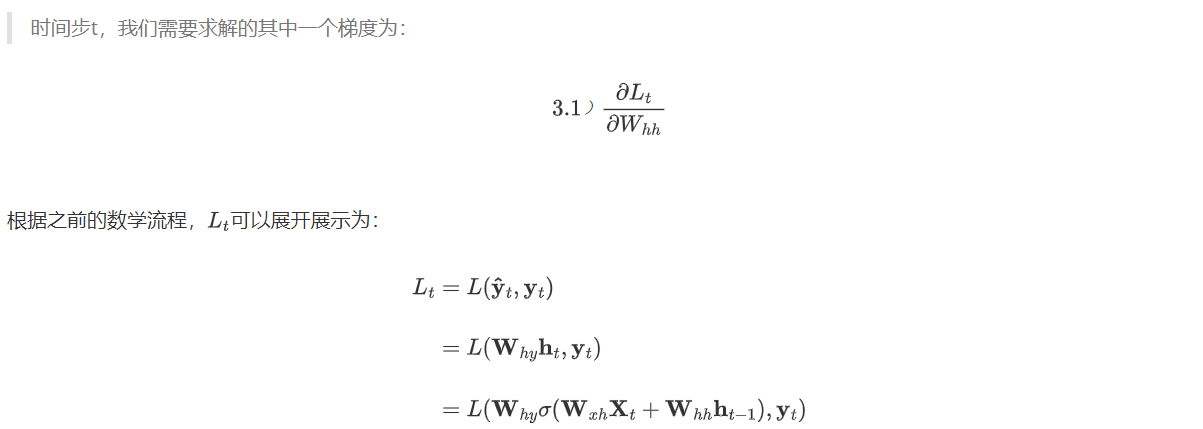


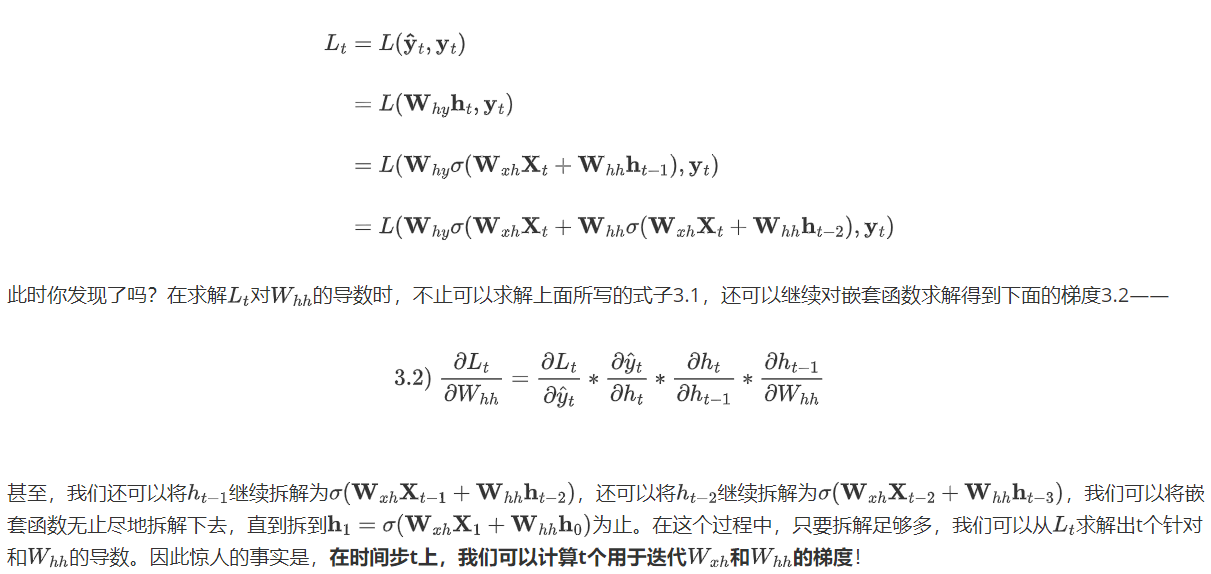


在深度神经网络中,在应用链式法则后,我们也会面临复合函数梯度连乘的问题,但由于普通神经网络中并不存在“权值共享”的现象,因此每个偏导数的表达式求解出的值大多是不一致的,在连乘的时候有的偏导数值较大、有的偏导数值较小,相比之下就不那么容易发生梯度爆炸或梯度消失问题的问题。
LSTM怎么解决梯度消失问题
你或许很早就听说过,LSTM能够很好地解决RNN的梯度消失/梯度爆炸问题,甚至你可能人为LSTM是为了解决梯度消失和梯度爆炸而诞生的,但我们在进行深度原理研究的过程中却发现并非如此。让我们来简单梳理一下LSTM的数学流程——

LSTM在反向传播中的梯度求解链路可以被可视化为:

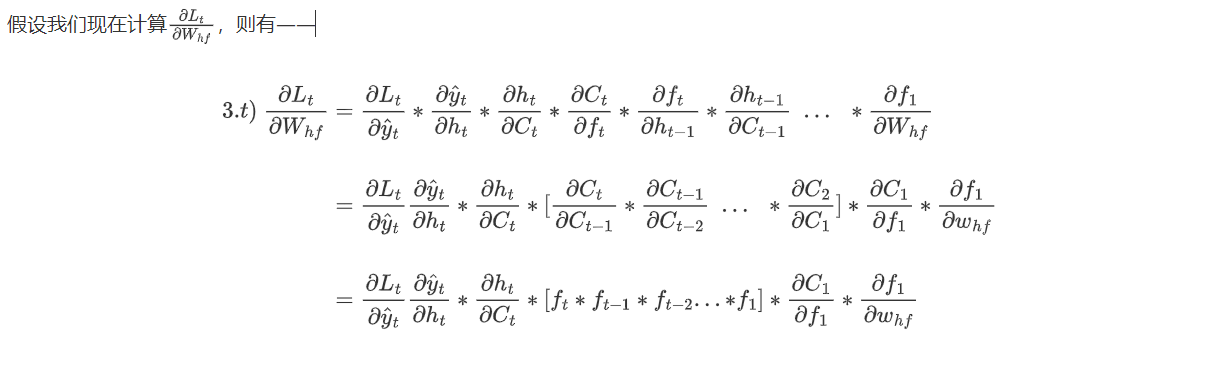

GRU结构
前向计算公式
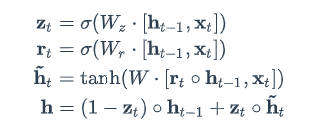
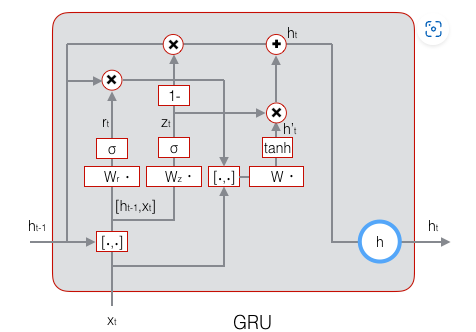
原理图
以后再看,累了





