希尔排序

希尔排序是特殊的插入排序。

他用来解决下面的问题：

当需要插入的数是较小的数时，后移的次数明显增多，对效率有影响。

算法原理

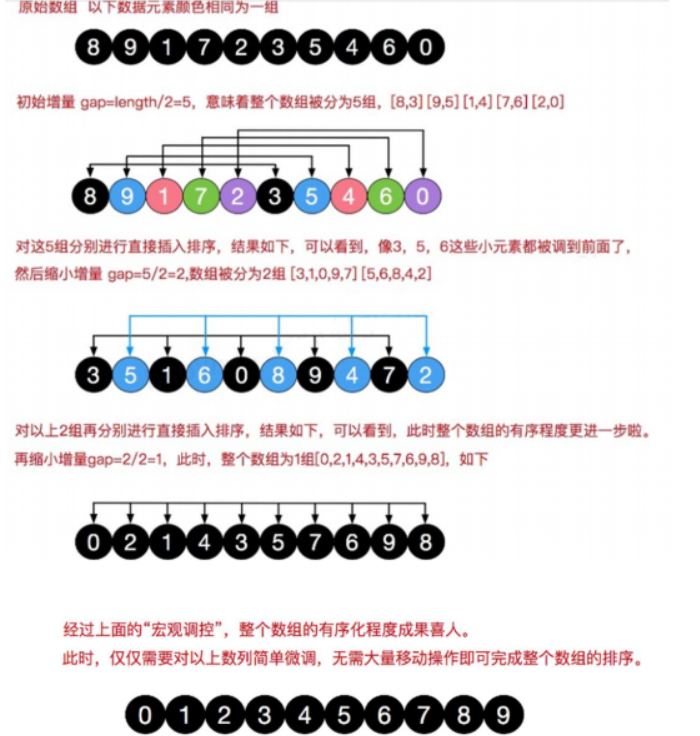
希尔排序也叫做缩小增量排序，希尔排序时把记录按照下标的一定增量分组，对每组使用插入排序算法排序；随着增量逐渐减小，每组包含的词也变小，当增量减为1时，整个文件被分为一组，算法结束。

import random
import time
def shell_sort(array):
    n = len(array)
    gap=n//2

    while gap > 0:
        for i in range(gap,n):
            temp=array[i]
            j=i
            while j>=gap and array[j-gap]>temp:
                array[j]=array[j-gap]
                j-=gap
            array[j]=temp
        gap//=2

#生成10000个值在0~10000的随机数
myList=[random.random()*10000 for i in range(10000)]
start_time=time.time()
shell_sort(myList)
print(myList)
#统计使用时间
print(f"--- {time.time() - start_time} seconds ---")

总用时0.07192134857177734 seconds

复杂度分析

步长的选择时希尔排序的重要部分，步长选择不同，最坏时间复杂度不同。当步长为2时，最坏时间复杂度为O(N^2)，当步长为2时，希尔排序会将相隔一个步长的元素分为一组，并对每个组进行插入排序。然后，步长减半，再次进行分组和插入排序。这个过程会持续进行，直到步长减至1，此时就变成了普通的插入排序。在最坏情况下，当列表中的元素按照逆序排列时，每个元素都需要在前面的已排序部分中逐个向前移动，直到找到合适的插入位置。这导致每个元素都需要进行大量的比较和移动操作。因此，当步长序列为2时，希尔排序的最坏时间复杂度为O(n^2)。