线性回归简介

线性回归是一种统计学习方法，用于建立自变量（特征）与因变量之间的线性关系，并通过拟合一个线性方程来预测连续的数值型因变量。线性回归在解释和预测数据方面具有广泛的应用。

简单线性回归模型的形式为：Y = XK + b，其中Y是因变量，X是自变量，K是模型的参数，b是截距。模型的目标是找到最佳的参数估计值（也就是K和b），使得模型预测值与实际观测值之间的误差最小化。

线性回归的基本假设是自变量与因变量之间存在线性关系，并且误差项服从正态分布。模型的核心思想是通过最小二乘法来估计参数，即最小化观测值与模型预测值之间的残差平方和。

使用情景

1. 预测分析：线性回归可以用于预测因变量的值。通过构建一个合适的线性回归模型，可以利用自变量的值来预测因变量的数值。例如：经典的波士顿房价预测
2. 关联分析：线性回归可以用于研究自变量与因变量之间的关联关系。通过分析回归系数的正负和大小，可以了解自变量对因变量的影响程度，进一步可以选择出对因变量更有影响的自变量。例如，分析广告投入与销售额之间的关系，以确定广告对销售的影响。
3. 异常检测：线性回归可以用于检测异常值。异常值可能会对回归模型的拟合产生较大的影响，因此通过分析残差（实际观测值与模型预测值之间的差异）可以识别出异常值。

线性回归假设自变量与因变量之间存在线性关系，并且对异常值和数据分布敏感，且只能用于处理线性关系的数据。

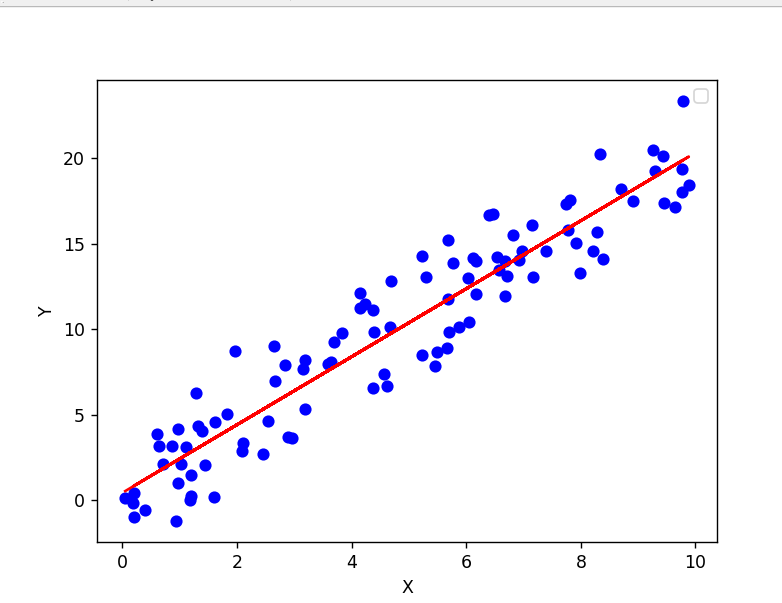
如上图所示根据自变量预测因变量，这个图整体呈现线性，所以就是线性回归。

什么是回归

回归是一种统计学方法，用于建立自变量与因变量之间的关系模型，并通过该模型进行预测或推断。回归分析旨在探索变量之间的关联性，以及使用自变量来预测或解释因变量的变化。

在回归分析中，自变量通常是输入或解释变量，而因变量是我们希望预测或解释的目标变量。回归模型通过拟合数据来估计自变量与因变量之间的关系，并提供关于因变量如何随着自变量的变化而变化的信息。回归分析的目标是找到最佳的参数估计值，以使回归模型的预测值与实际观测值之间的误差最小化。常见的回归方法包括线性回归、多项式回归、岭回归、Lasso回归等，而逻辑回归则是属于分类。

回归的使用场景有预测分析，比如：波士顿房价预测，关联分析，异常分析等。

线性回归原理

线性回归方程

线性回归基本原理是通过拟合一个线性方程，找到最佳的参数估计值，以最小化观测值与模型预测值之间的误差。

假设我们有一个自变量 X 和一个因变量 Y，线性回归的基本形式可以表示为：
$$Y=XK+b$$
其中，Y 是因变量，X 是自变量，K和b是模型的参数，b称为截距，表示当自变量 X 等于 0 时，因变量 Y 的值。K称为斜率，表示 Y 随着 X 的变化而变化的速率。你可能会说，这个东西我上小学就会了，你在搞什么飞机。这个地方各个变量都不再是我们小学学的一个特定的值，都是矩阵。我们可以看到我的大写字母就是表示矩阵，小写的b就是表示标量。但是大差不差，道理是一样的。

我们假设自变量中有3个特征，而我们X中有4个小样本，那么我们的X，应该是4*3的矩阵；而我们的k只需要处理3个特征，所以他应该是3*1的矩阵；Y应该是4*1的矩阵，表示在下图。
$$X=\left[\begin{array}{ccc}{x}_{11}& x_{12}& x_{13}\\ x_{21}& x_{22}& x_{23}\\ x_{31}& x_{32}& x_{33}\\ x_{41}& x_{42}& x_{43}\end{array}\right],K=\left[\begin{array}{c}{k}_{11}\\ k_{21}\\ k_{31}\end{array}\right],Y=\left[\begin{array}{c}{y}_{11}\\ y_{21}\\ y_{31}\\ y_{41}\end{array}\right],b=b$$
我们要用这个公式取推导出预测值，就是推出合适的K和b，我们先根据上面的公式运算一遍，相信大家都应该知到矩阵的运算。
$$XK+b=\left[\begin{array}{c}{x}_{11}\ast k_{11}+x_{12}\ast k_{21}+x_{13}\ast k_{31}+b\\ x_{21}\ast k_{11}+x_{22}\ast k_{21}+x_{23}\ast k_{31}+b\\ x_{31}\ast k_{11}+x_{32}\ast k_{21}+x_{33}\ast k_{31}+b\\ x_{41}\ast k_{11}+x_{42}\ast k_{21}+x_{43}\ast k_{31}+b\end{array}\right]$$

我们想要这个结果的值等于Y，也就是对应相等，自变量我们无法改变，所以就是通过调整K的值来让XK+b的值等于Y。那我们直接用Y-(XK+b)，得到残差值，然后使用最小二乘法使得残差值平方和最小，这个残差值平方和最小，那么预测值和真实值的差距也就越小。

最小二乘法求解线性回归

损失函数（Loss function）是机器学习中用于衡量模型预测值与实际观测值之间差异的函数。它是模型优化的关键组成部分，用于度量模型在给定数据上的性能。在监督学习任务中，我们通常有一个训练集，其中包含输入特征和对应的目标变量（实际观测值）。模型的目标是根据输入特征预测目标变量。损失函数衡量了模型预测值与实际观测值之间的差异，即模型的误差。

在上面的例子中，我们的损失函数就是最小二乘法求解的残差值平方和最小，也即是：
$$loss=\sum _{i=1}^4(y_i-x_i\ast K-b{)}^2或者loss=(Y-XK-b{)}^T(Y-XK-b)$$
其中y_i表示y的一行，也即是y的行向量；x_i表示x的一行，也即是x的行向量；b是公用的；T表示对矩阵的转置。

下面我们的目标就是最小化损失函数。我们先对损失函数求偏导数，献丑了（字不咋滴）

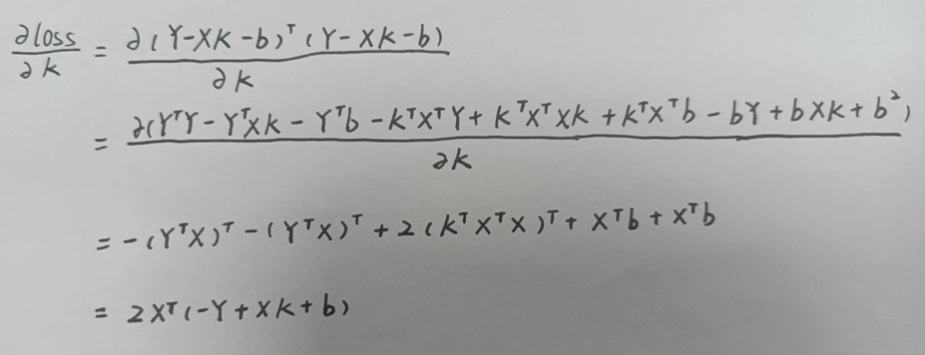
然后零偏导数等于0求得K的值
$$K=\frac{Y-b}{X}$$

对于上面的例子，我们知道Y和X，但是b的引入是不足以让我们计算出K的，在sklearn中，可以帮助我们自动计算，b也是一个定值。

直接使用这个公式可以方便计算出线性回归的K值。最小二乘法适用于小规模数据集和简单模型。那么我们还有什么方法求解线性回归呢？

梯度下降求解线性回归

我们还可以使用梯度下降算法求解线性回归。我们将上面选取K和b对应的损失函数记为loss(K,b)，那么loss(K,b)与K或者b的关系应该是什么呢？我们可以将损失函数和K的关系形象化为下面的图：

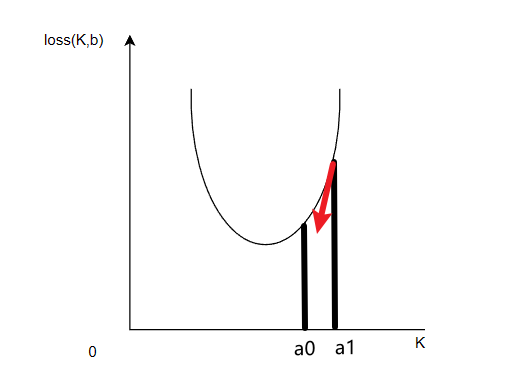
对于曲线上的任意一个k，沿着loss导数的反方向慢慢移动，也就是图像上点的斜率的反方向，最终有一天loss的值会到达最小值，loss导数是什么呢？也就是下面的值：
$$\frac{\mathrm{\partial }loss(K,b)}{\mathrm{\partial }K}$$
移动的斜率我们已经知道了，但是移动的步长是多少呢？我们定义一个变量α为移动的步长，我们每次更新k按照下面的方式：
$$k_{new}=k_{old}-\alpha \ast \frac{\mathrm{\partial }loss(K,b)}{\mathrm{\partial }K}$$
我们在更新k值的时候需要考虑，每次移动的速度，我们成为α，也叫做“学习率”。当我们刚开始训练时，可以适当增大学习率，可以加速参数逼近最优的情况，当我们快到达函数的底端时，我们要减少消息率，保证函数收敛。

这就是梯度下降算法，也是线性回归常用的解决方法。实际上，我们在训练模型时，不需要手动编写复杂的梯度计算，sklearn已经帮我们实现了，下一章我们将进行介绍。

线性回归特点

优点：

1. 简单而直观：线性回归模型非常直观，易于理解和解释。它通过拟合一条直线或超平面来建立变量之间的线性关系，因此结果具有可解释性。
2. 计算效率高：线性回归的计算复杂度较低，求解参数的闭式解（最小二乘法）可以高效地计算，而且对于大规模数据集也能快速进行训练。
3. 可解释性好：线性回归模型提供了每个特征的权重系数，可以用于解释变量之间的关系和影响程度。这使得线性回归在某些领域（如经济学和社会科学）中非常有用。

缺点：

1. 假设限制：线性回归假设自变量和因变量之间存在线性关系。如果实际关系是非线性的，线性回归模型可能无法很好地拟合数据，导致预测性能较差。
2. 对异常值敏感：线性回归对异常值（在因变量或自变量中的极端值）比较敏感，这可能会导致模型的拟合结果受到较大影响。
3. 多重共线性：当自变量之间存在高度相关性时，线性回归模型可能会受到多重共线性的影响。这会导致参数估计不准确，增加模型的不稳定性，并降低模型的可解释性。