贝叶斯简介

贝叶斯统计学的发展脉络可以追溯到18世纪，起源于托马斯·贝叶斯（Thomas Bayes）对概率和统计的研究。

1. 贝叶斯定理的提出：贝叶斯定理是贝叶斯统计学的核心，它最早由托马斯·贝叶斯在1763年发表的一篇文章中提出。贝叶斯定理描述了在已知先验概率的情况下，如何根据新的观测数据来更新对模型参数的估计。
2. 在贝叶斯统计学的发展过程中，出现了两种主要的统计学观点：频率主义和贝叶斯主义。频率主义将概率解释为事件发生的频率，强调通过大量的重复观测来估计模型参数。而贝叶斯主义将概率解释为对事件的主观信念或不确定性的度量，强调通过先验知识和观测数据来更新模型参数的概率分布。
3. 贝叶斯统计学的发展：贝叶斯统计学在20世纪逐渐得到发展和推广。但由于计算复杂性和先验选择的问题，贝叶斯方法在实际应用中受到限制。直到20世纪80年代，随着计算机技术的进步和马尔科夫链蒙特卡洛（MCMC）方法的引入，贝叶斯统计学才开始显现出更大的潜力和实用性。

使用情景

贝叶斯算法在处理不确定性和进行推断的任务中，应用较多。

1. 模式识别和分类：贝叶斯分类器是一种常见的机器学习算法，用于将数据点分到不同的类别中。它基于贝叶斯定理，通过计算给定观测数据的条件下，每个类别的后验概率来进行分类预测。贝叶斯分类器常用于文本分类、图像识别、垃圾邮件过滤等任务。
2. 推荐系统：贝叶斯方法可以用于个性化推荐系统。通过建立用户和物品之间的概率模型，结合用户的观测数据和先验知识，可以预测用户对未观测物品的兴趣，从而提供个性化的推荐。

贝叶斯原理

贝叶斯理论基础基于贝叶斯定理和条件独立性假设。对于给定的数据集：
$$T=\{(x_1,y_1),(x_2,y_2),\dots \dots ,(x_n,y_n)\}$$
对于任意的输入x，利用贝叶斯定理求出后验概率最大的P(Y|X=x)对应的y的取值。

条件概率

条件概率就是指在A发生的情况下，B发生的概率，用P(B|A)来表示。如下文氏图：

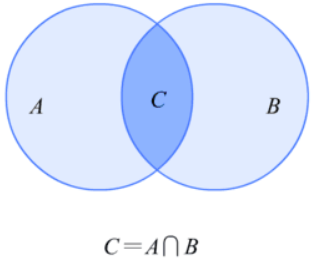
我们可以很清晰的看到在P(B|A)就是等于P(C)除以P(A)，下面的公式就是条件概率公式。
$$P(B|A)=\frac{P(A\cap B)}{P(A)}$$

全概率公式

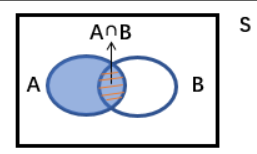
在S全体空间中，分为A和A’两个部分，那么P(B)怎么表示呢，它是等于在A发生条件下B发生的概率乘以P(B)再加上在A‘发生条件下B发生的概率乘以P(B’)，就是下面的公式
$$P(B)=P(B|A)\ast P(A)+P(B|A^{\prime })\ast P(A^{\prime })$$

贝叶斯公式

在条件概率上稍加变形，如下所示：
$$\begin{gathered} P(B|A)=\frac{P(A\cap B)}{P(A)} \\ so：P(A\cap B)=P(A)P(B|A)=P(B)P(A|B) \\ so：P(A|B)=\frac{P(B|A)P(A)}{P(B)} \end{gathered}$$
最后一个公式就是贝叶斯公式。

我们称P(A)为先验概率，是我们已经事先知道的。P(A|B)为后验概率，即是在B发生条件下，A发生的概率。P(B|A)P(B)为可能性函数，这相当于一个调整因子。

所以可以写成：后验概率=先验概率*调整因子

当可能性函数P(B|A)P(B)大于1时，先验函数被增强，事件A发生的可能性变大；可能性函数等于1时表示B事件和A时间是无关系的，没有影响；当可能性函数小于1时，先验概率被削弱，事件A的可能性变小。

朴素贝叶斯

朴素贝叶斯是一种理想的情况，它假设输入的各个特征之间没有关系，实际上很难达到这个效果，为什么需要这个理想情况呢，我们看一个例子。

我们使用挑西瓜来举例，西瓜有x₁，x₂，x₃三个特征，所以贝叶斯公式可以写成下面的样子：
$$P(y|x_1,x_2,x_3)=\frac{P(x_1,x_2,x_3|y)P(y)}{P(x_1,x_2,x_3)}$$
由于条件概率分布有指数及数量的参数，因此，求解该问题是一个NP难问题，实现中很难解决，所以直接求解不可行。所以朴素贝叶斯对条件概率做了条件独立性的假设。也即是下面的公式
$$P(y|x_1,x_2,x_3)=\frac{P(x_1|y)P(x_2|y)P(x_3|y)P(y)}{P(x_1,x_2,x_3)}$$

拉普拉斯平滑

算法还存在什么问题呢？我们要计算多个概率的乘积获取西瓜属于某个类别的概率，也即是P(x~1~|y)P(x~2~|y)P(x~3~|y)，如果其中有一个概率值为0，那么最后的结果一定为0，那么最终西瓜属于某个类别的概率一定也是0了，显然这是不合理的，为了降低这种影响，我们可以把所有特征值出现的次数初始化为1，并把类别上加上3。加上1是为了平滑，确保概率不为0，在分母上加上3是为了将概率总和调整为1。

这个和之前的SVM加上软分隔非常类似。

朴素贝叶斯的优缺点

优点：

1. 简单快速：朴素贝叶斯算法具有简单的计算过程，易于实现和理解。它通常在处理大规模数据时表现出色，并且训练和预测的速度都很快。
2. 高效性：由于朴素贝叶斯算法假设特征之间是条件独立的，它只需要学习每个特征的单独概率分布，而不需要考虑特征之间的复杂关系。这导致了较低的计算复杂度和存储需求。
3. 对小样本数据有效：朴素贝叶斯算法在小样本数据集上表现良好，因为它可以通过利用特征条件独立性的假设来估计参数，减少对数据的依赖。
4. 可解释性强：朴素贝叶斯算法提供了直观的概率框架，可以解释分类结果的原因。它可以告诉我们每个特征对于分类的贡献程度，帮助理解和解释模型。

缺点：

1. 特征独立性假设：朴素贝叶斯算法假设所有特征之间是相互独立的，这在现实问题中往往不成立。这个假设可能导致模型无法捕捉特征之间的复杂关系，从而影响分类准确性。
2. 对输入数据分布敏感：朴素贝叶斯算法假设特征的概率分布是已知的，如果输入数据的分布与模型的假设不匹配，可能会导致较低的分类准确性。