深度学习一:人工神经网络
人工神经网络
人工神经网络(Artificial Neural Network,ANN)是一种受到生物神经系统启发的机器学习模型。它由大量的人工神经元(也称为节点或单元)组成,这些神经元之间通过连接(也称为权重)相互交互和传递信息。
人工神经网络通常由三个主要部分组成:
- 输入层(Input Layer):接受外部输入数据,将其传递给网络的中间层。
- 中间层(Hidden Layer):也称为隐藏层,由多个神经元组成。中间层可以有一个或多个,每个神经元都与前一层和后一层的神经元相连。
- 输出层(Output Layer):从中间层接收信息,并生成网络的输出结果。
人工神经网络的工作过程如下:
- 初始化网络:设置神经元之间的连接权重和偏置(用于调整神经元的激活阈值)。
- 前向传播(Forward Propagation):将输入数据通过网络,从输入层传递到输出层。每个神经元将输入与其连接权重相乘,并将结果传递给激活函数进行处理,产生激活值。
- 激活函数(Activation Function):激活函数决定神经元是否激活,并将激活值传递给下一层。常见的激活函数包括Sigmoid、ReLU、Tanh等。
- 计算输出:输出层的神经元根据激活函数的输出生成最终的网络输出。
- 反向传播(Backpropagation):根据网络输出和预期输出之间的差异(损失函数),通过梯度下降算法来调整连接权重和偏置,以最小化损失。反向传播通过将误差从输出层反向传播到隐藏层和输入层来更新权重。
- 重复迭代:重复进行前向传播和反向传播,直到达到预定的停止条件(例如,达到最大迭代次数或损失函数收敛)。
神经元模型
神经元模型连接形成神经网络,神经元接受来自其他n个神经元传递过来的信号,这些输入信号通过带有的权重的连接进行传递,神经元接受到的总输出值与阈值进行比较,然后通过激活函数处理产生神经元的输出。
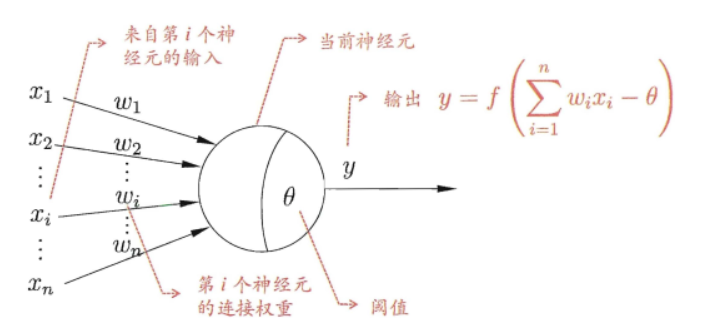
最符合人脑神经元的激活函数是阶跃函数,它将输入值映射为输出值”0″和”1″,分别对应着神经元抑制和兴奋,但是阶跃函数具有不连续,不光滑的性质,因此常用的激活函数是sigmoid函数。
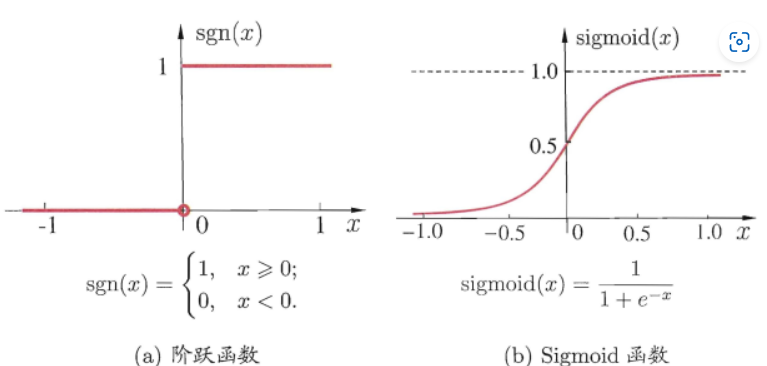
把许多个这样的神经元按照一定的层次进行连接,得到了神经网络。
为什么需要激活函数
- 引入非线性:激活函数将输入信号转换为输出信号,并引入了非线性的变换。如果没有激活函数,多层神经网络就只是一系列线性变换的叠加,无法表达更复杂的非线性关系。通过使用非线性激活函数,神经网络可以学习和表示更复杂的数据模式。
- 提升神经网络的表示能力:激活函数的非线性特性增加了神经网络的表示能力。它们允许网络学习非线性特征和决策边界,从而更好地拟合各种复杂的数据分布。
- 梯度传播:激活函数的选择直接影响到反向传播算法中的梯度传播。激活函数应具有可导性,以便梯度可以传递回网络的较早层,从而使得网络可以学习调整权重和提高性能。
什么样的函数可以作为激活函数
根据万能逼近定理,只要激活函数选择得当,神经元个数足够多,使用3层即包含一个隐藏层的神经网络就可以实现对任何一个从输入向量到输出向量的连续映射函数逼近。
为了保证网络可以学习到非线性特征,激活函数必须是非线性函数,但是仅仅有非线性是不行的。梯度下降法需要计算损失函数对参数的梯度值,这个梯度值根据上面的误差项计算,而误差项的计算又涉及到计算激活函数的导数,因此激活函数必须是可导的。
没有激活函数的神经网络
如何评价激活函数
反向传播算法计算误差项的时候每一层都需要乘以本层激活函数的导数。如果激活函数导数的绝对值小于1,多次连乘之后误差项会衰减到0,参数的梯度值由误差项计算得到,从而导致前面层的权重梯度接近0,这就是梯度消失。与之相反的是梯度爆炸,如果激活函数导数的绝对值大于1,多次乘积之后权重值会趋向于非常大的数,这就是梯度爆炸。
激活函数饱和性概念,如果一个激活函数满足:
则称该函数为右饱和,类似的如果满足:
则称函数为左饱和,如果一个函数既满足左饱和又满足右饱和,称之为饱和。如果存在常熟c,当x>c的时候有:
则称函数为右硬饱和,当x<c时有:
则称函数为左硬饱和,既满足左影饱和又满足右硬饱和的函数成为硬饱和函数。饱和性和梯度小时问题密切相关。在反向传播过程中,误差项在每一层都要乘以激活函数导数值,一旦x的值落入饱和区间,多次乘积之后会导致梯度越来越小,从而出现梯度消失问题。
sigmoid函数的图像是:
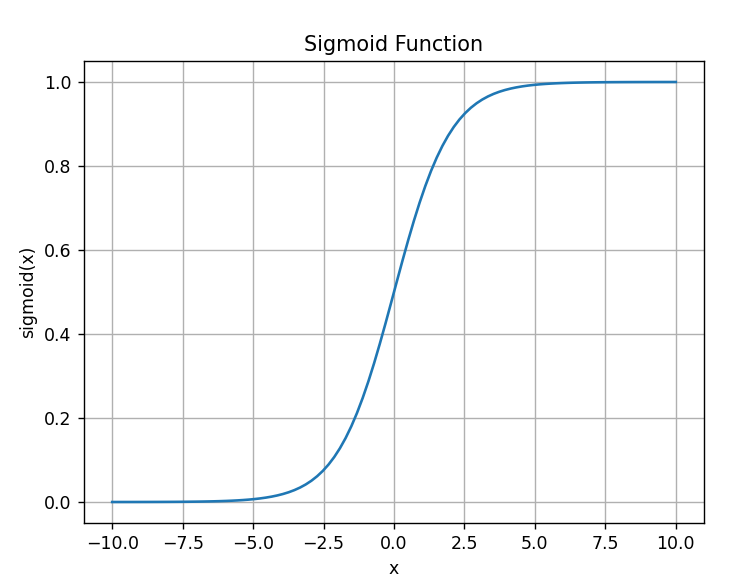
sigmoid函数输出映射为(0,1)之间,单挑连续求导简单,但是其饱和性,容易产生梯度消失。tanh函数的表达式是:
它的图象是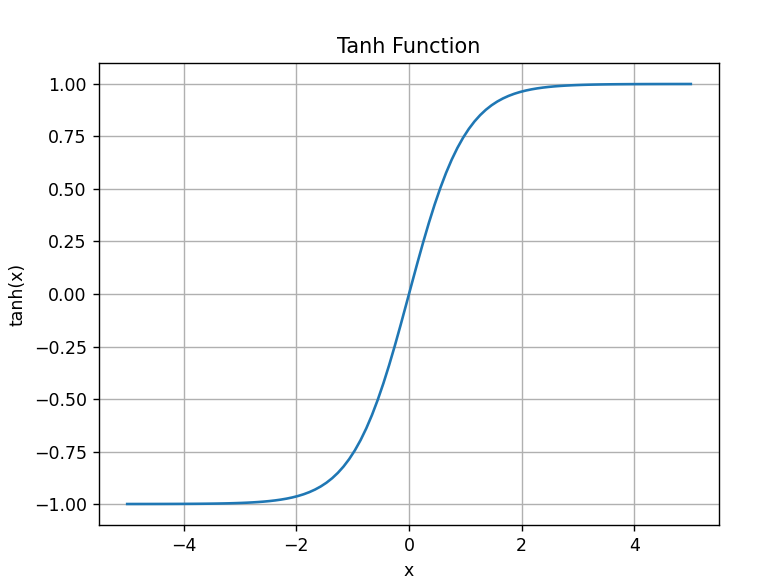
tanh函数的输出值以0为中心,位于(-1,1)之间,相比于sigmoid函数训练时收敛速度更快,但是它还是饱和函数,存在梯度消失问题。
relu函数其形状为一条折线,当x<0的时候做截断处理。该函数在0点处不可导,如果忽略这个点,它的导数为sgn。函数的导数计算简单,能解决梯度消失的问题。
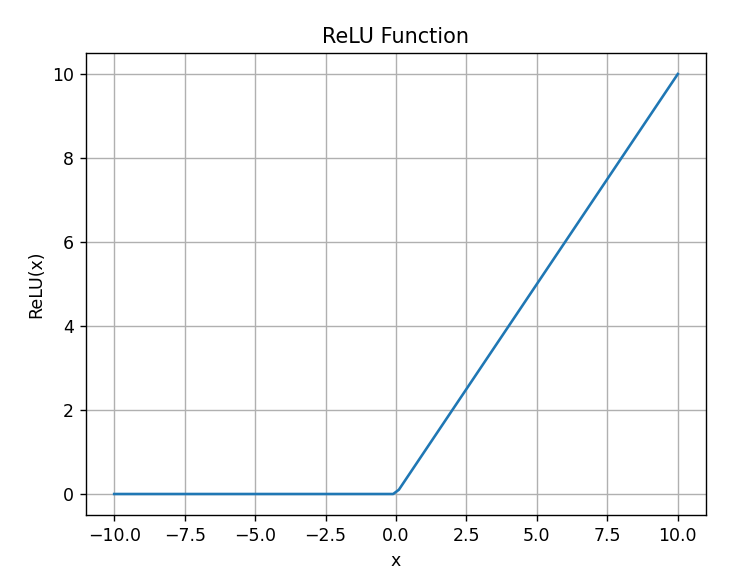
ReLU函数的特点如下:
- 非线性:ReLU函数是一种非线性激活函数,能够引入非线性因素,增加模型的表达能力。相比于线性激活函数,如线性函数或sigmoid函数,ReLU能够更好地拟合复杂的数据模式。
- 稀疏激活性:在ReLU函数中,当输入值小于 0 时,输出为 0,这意味着部分神经元将被“激活关闭”,不会参与信息传递。这种稀疏激活性可以使模型具有更高的表示能力和泛化能力。
- 计算高效:ReLU函数的计算非常简单,只需比较输入值与 0 的大小即可,没有复杂的数学运算。这使得ReLU函数的计算速度快,适合大规模的深度学习模型。
然而,ReLU函数也存在一些问题:
- 死亡神经元问题(Dead Neurons Problem):当输入值为负时,ReLU函数的导数为 0,导致神经元无法更新权重。如果大量神经元处于这种状态,它们将无法激活,导致网络的部分功能丧失。
- 输出不是以 0 为中心:ReLU函数的输出范围是 [0, +∞),缺乏负值输出。这可能导致某些情况下网络的不稳定性,需要采取一些处理措施,如批归一化(Batch Normalization)
感知机
感知机由两层神经元组成,输入层接收输入信号后传递给输出层,输出层是MP神经元,也叫做与之逻辑单元。
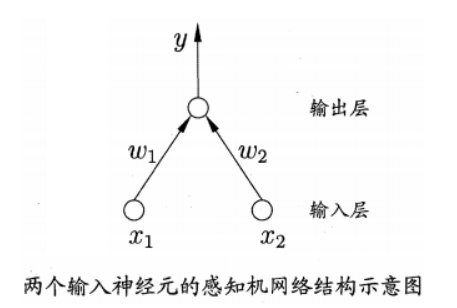
感知机能容易实现逻辑与,或,非运算,注意到
假设f是激活函数中的阶跃函数,那么有
- “与”(x1 && x2):令w1 = w2 = 1,θ = 2,则y = f( 1·x1 + 1·x2 – 2 ),仅在x1 =1且x2 = 1时,y = 1
- “或”(x1 || x2):令w1 = w2 = 1,θ = 0.5,则y = f( 1·x1 + 1·x2 – 0.5 ),当x1 = 1或x2 = 1时,y = 1
- “非”(! x1):令w1 = -0.6,w2 = 0,θ = -0.5,则y = f( -0.6·x1 + 0·x2 + 0.5 ),当x1 = 1时,y = 0;当x1 = 0时,y = 1
多层感知机
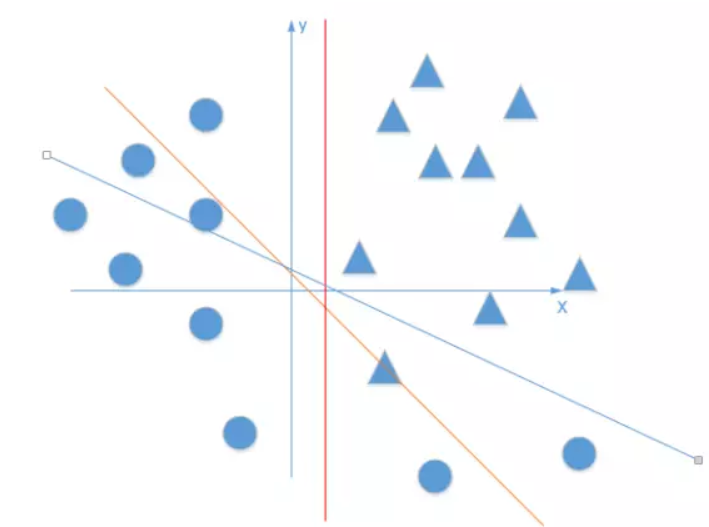
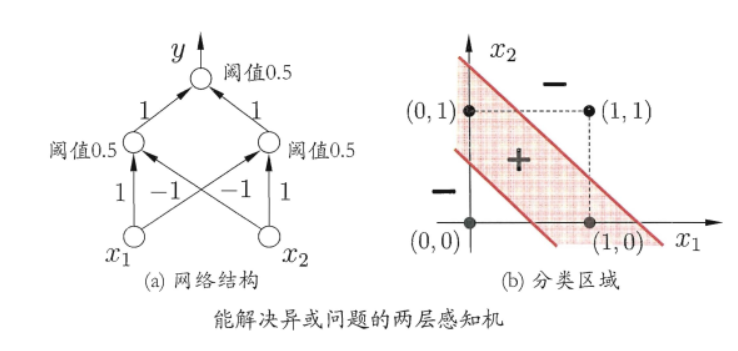
感知机只有输出层神经元进行激活函数处理,即只拥有一层神经单元,学习能力非常有限,并且只能解决线性可分的问题,就是一个超平面即可划分,如下图所示。
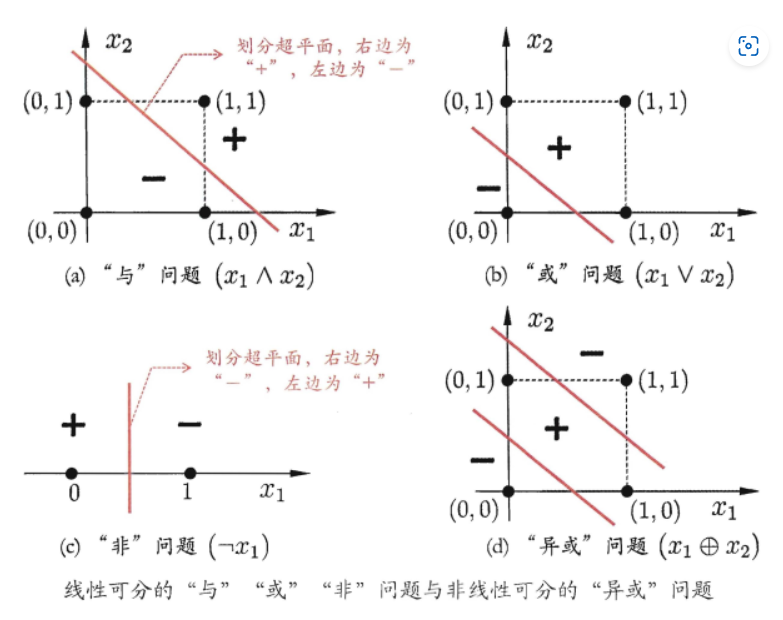
对于d,要解决线性不可分的问题,需要考虑多层感知机,例如下图中的两层感知机就能解决异或问题。如下图所示,输入层和输出层之间的一层神经元,成为隐藏层神经元,隐藏层神经元和输出层神经元都是拥有激活函数的功能神经元。
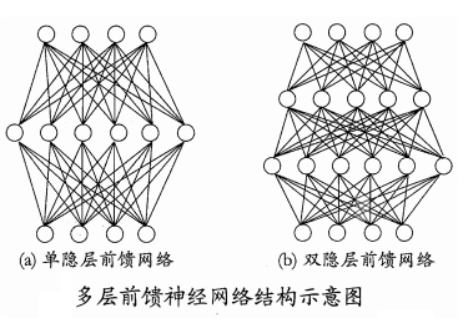
更一般的,常见的神经网络是形如下图所示的层级结构,每层神经元与下层神经元全互连,神经元之间不存在同层连接, 也不存在跨层连接。这样的神经网络结构通常称为”多层前馈神经网络“(multi-layer feedforward neural networks),其中输入层神经元接收外界输入,隐层与输出层神经元对信号进行加工,最终结果由输出层神经元输出;换言之,输入层神经元仅是接受输入,不进行函数处理,隐层与输出层包含功能神经元。因此,下图(a)通常被称为”两层网络”。为避免歧义,本书称其为”单隐层网络”。只需包含隐层,即可称为多层网络。神经网络的学习过程,就是根据训练数据来调整神经元之间的”连接权值”以及每个功能神经元的阈值;换言之,神经网络”学”到的东西,蕴涵在连接权值与阈值中。
BP算法
给定训练集D = { (x1, y1), (x2, y2), … , (xm, ym) },即输入示例由d个属性描述,输出l维实值向量。
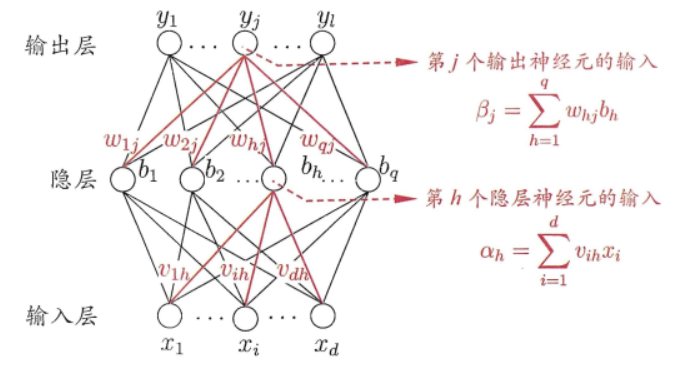
为便于讨论,下图给出了一个拥有d个输入神经元、l个输出神经元、q个隐层神经元的多层前馈网络结构,其中输出层第j个神经元的阈值用θj表示,隐层第h个神经元的阈值用γh表示。输入层第i个神经元与隐层第h个神经元之间的连接权为v(ih),隐层第h个神经元与输出层第j个神经元之间的连接权为w(hj)。
对于训练个例(xk,yk),假设神经元的输出为:
即
则网络在(x~k~,y~k~)上的均方差损失为
其中,添加1/2是为了后续求导的便利。
上面的网络中一共有:输入层到隐层的d*q个参数、隐层到输出层的q*l个参数,q个隐层神经元的阈值,l个输出层神经元的阈值。BP是一个迭代学习算法,在迭代每一轮中采用广义的感知机学习规则对参数进行更新。参数更新估计式为。
我们使用隐层到输出层的连接权重w(hj)进行推导。
BP算法基于梯度下降策略,以目标的负梯度方向对参数进行调整,对于上式的均方误差Ek,给定学习率$eta$,有:
注意到w(hj)先影响到第j个输出层神经元的输入值$beta$j,再影响输出层的输出,所以有:
根据定义,有:
sigmoid激活函数有一个很好的性质:
于是有输出层的灵敏度gj为
所以BP算法中关于输出层的权值的w(hj)的更新公式为:
输出层的阈值$theta$~j~更新公式为
类似可以得到隐层灵敏度为:

学习率η∈(0, 1)控制着算法每一轮迭代中的更新步长(常设置为η = 0.1),若太大则容易振荡,太小则收敛速度又会过但。有时为了做精细调节,可分别在每层设置不同的学习率。
下图给出了BP算法的工作流程。对每个训练样例,BP算法执行以下操作:先将输入示例提供给输入层神经元,然后逐层将信号前传,直到产生输出层的结果;然后计算输出层的误差(第4-5行),再将误差逆向传播至隐层神经元(第6行),最后根据隐层神经元的误差来对连接权和阈值进行调整(第7行)。该迭代过程循环进行,直到达到某些停止条件为止,例如训练误差己达到一个很小的值(停止条件与缓解BP过拟合的策略有关)

因为神经网络强大的学习能力,BP神经网络京城出现过拟合的问题,其训练误差持续降低,但是测试误差却上升,有两种方法缓解BP网络的过拟合:
第一种就是“早停”。第二种是正则化,基本思想是在误差目标函数中增加一个用于描述网络复杂度的部分,例如连接权与阈值的平方和。仍令Ek表示第k个训练样例上的误差,wi表示连接权和 阈值,则误差目标函数改变为:
其中λ∈(0, 1)用于对经验误差与网络复杂度这两项进行折中,常通过交叉验证法来估计。
增加连接权与阈值平方和这一项后,训练过程将会偏好比较小的连接权和阈值,使网络输出更加”光滑”,从而对过拟合有所缓解。
全局最小和局部最小
若用E表示神经网络在训练集上的误差,则它显然是关于连接权重w和阈值$theta$的函数。此时神经网络的训练可以看作一个参数寻优的过程,在参数空间中,寻找一组最优参数使得E最小
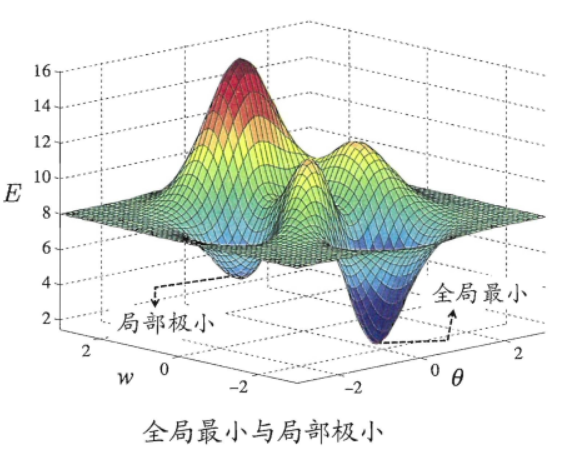
基于梯度的搜索是使用最为广泛的参数寻优方法。如果误差函数具有多个局部极小,则不能保证找到解是全局最优,我们尝试跳出局部最小,进一步接近全局最小。
- 使用随机梯度下降。与标准梯度下降法精确计算梯度不同,随机梯度下降法在计算梯度加入了随机因素。于是,即便陷入到局部极小点,也可以让梯度不为0,有机会跳出来。
- 退火模拟,在每一步都以一定的概率接收比当前解更差的结果,从而有助于跳出局部最小。在每次迭代过程中,接受次优解的概率随着时间的推移逐渐降低,从而保证算法的的稳定性
- 以多组不同参数值初始化多个网络,按照标准方法训练之后,取其中误差最小的解作为最终参数,这相当于从多个不同的初始值开始搜索,这样就可能陷入到不同的局部极小,从中选择有可能的获得全局最小结果





It is appropriate time to make some plans for the
future and it’s time to be happy. I’ve read this post and if I could I wish to
suggest you few interesting things or suggestions.
Maybe you could write next articles referring to this article.
I want to read even more things about it!
It is the best time to make some plans for the future and it is time to be happy.
I have read this post and if I could I want to suggest you some interesting things or
tips. Perhaps you could write next articles referring to
this article. I want to read more things about it!